图的概述
图是一种很重要且很普遍的数学模型,现实生活当中很多问题都可以用图来刻画,然后利用图的相关算法加以解决,比如:
- 路径规划,城市之间的公路网,寻找 A 城市到 B 城市之间的最短路径
- 社交网络,分析共同爱好等
图的存储结构
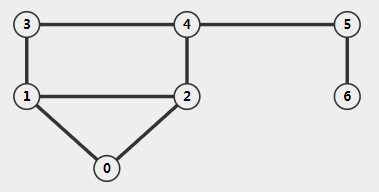
三种存储结构:邻接矩阵,邻接表,边集数组
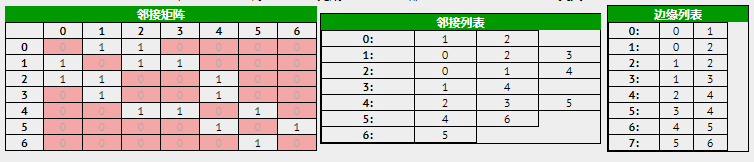
无向图
单点连通性,找出与目标顶点所有连接的顶点
思路:DFS 遍历,用顶点数组变量标记是否访问
单点路径查找,找出与目标顶点的路径
思路:DFS 遍历,用顶点数组变量标记每个顶点的父顶点,然后从终止顶点向上查找直到找到起始节点
单点最短路径
思路:队列实现 BFS 遍历,其他跟路径查找一样
连通分量,求一幅图中所有的连通分量,可判断任意两点是否连通,常数时间的查询
思路:DFS 遍历,用顶点数组变量标记每个顶点所属的连通分量
判断是否有环
思路:DFS 遍历,一个顶点被访问 2 次,则有环
二分图(双色问题)
思路:DFS 遍历,每个顶点染相反的颜色
有向图
与无向图中的问题类似
单点可达性、多点可达性、单点路径查找、单点最短路径
DAG,检测有向图是否有环,并打印环
DFS 遍历的顶点排序:前序排列,后序排列,逆后序排列
拓扑排序定义:给定一副有向图,将所有顶点排序,使得所有的有向边均从排在前面的元素指向后面的元素
拓扑排序,就是 DFS 的逆后序排列
当且仅当有向图是有向无环图时,才有拓扑排序,所以需注意拓扑排序前检测是否有环
强连通性:如果两顶点互相可达,则为强连通的,一幅图中任意两点都是强连通的,则有向图也是强连通的
强连通分量:有向图中被分为几个子图,每个子图中的顶点均为强连通的
求强连通分量:kosaraju 算法,待研究
顶点对的可达性:判断任意两顶点是否可达,要求常数时间的查询
传递闭包算法,待研究
最小生成树(加权无向图)
生成树:包含所有顶点的无环连通子图
加权无向图:权值最小的生成树为最小生成树
加权有向图:有向图的最小生成树为最小树形图,不研究
求最小生成树的算法
切分定理:在一幅加权图中,给定任意的切分,它的横切边中的权重最小者必然属于图的最小生成树。
- Prim 算法,加点法,每次选择跟树最近(权值最小)的非树顶点加入树中
- Kruskal 算法,加边法,所有边按权值排序,每次选择权值最小的边,并且边的两个顶点不属于同一棵树,添加到树中,直到 n-1 条边或所有边都属于同一颗树
最短路径(加权有向图)
最短路径树:给定起点,到其他所有顶点最短路径的树
- dijkstra 算法,同 prim 算法,每次选择跟树最近的边加入,一个数组保存起点到其他点的最短距离,一个数组保存当前顶点最短距离的边的信息,一个队列保存访问过的顶点
- 拓扑排序最短路径算法,按照拓扑排序的顺序添加边,得到拓扑排序中第一个顶点到其他顶点的最短路径,对于给定的起点的最短路径,拓扑排序中起点前的顶点都是不可达的。
- bellman-ford 算法,待研究
最长路径:权值取反求最短路径
优先级限制下的任务调度问题:
单处理器:有向图无环图的拓扑排序
多处理器:关键路径法,求有向图中的最长路径
dijkstra 算法只适用权值非负的有向图
拓扑排序最短路径算法 适用于无环有向图,可处理负权值
bellman-ford 算法,不能存在负权重环